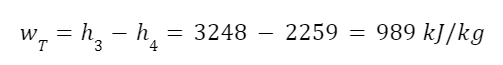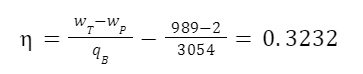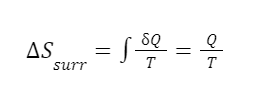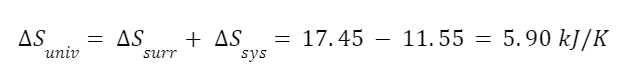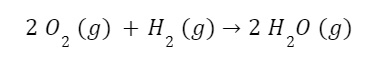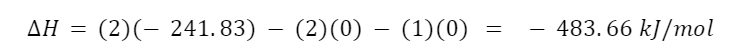The question “How many angels can dance on the head of a pin?” is typically used as a mocking retort to the sorts of philosophical and especially theological questions that are thought to be of little usefulness and a general waste of effort. It’s especially used in reference to philosopher theologians of the Middle Ages like Scholastics including Thomas Aquinas and Duns Scotus. While the material conditions of people in the world were those of misery and squalor (so it is supposed) these folks were sitting in their ivory towers thinking about useless questions instead of doing science and inventing things. As you might guess, I don’t share this perspective and as a kind of subversion of the retort I’d like to appropriate it. The question “How many angels can dance on the head of a pin?” is not a question anyone actually ever asked. It’s a straight up caricature. But Medieval Scholastic philosophy did have plenty of talk about angels. Why? And could angels have any modern intellectual relevance?
In what follows I propose that angels were used in Medieval Scholastic philosophy as subjects for thought experiments. In such thought experiments the properties of angels were not those primarily of angels as described in biblical texts but more of an idealized notion serviceable to philosophical exercises. I propose that these sorts of philosophical angels can still be used to explore questions we find interesting today in thought experiments pertaining to cognition and consciousness. With an understanding of thought experiments as idealizations which transcend particularity in order to achieve generality I’ll go through various stages of generalization of consciousness from its particular human form to its most general form. This process moves into the complete abstraction of consciousness from any of its particular physical instantiations in order to explore its most essential features, though with our present knowledge this can only be the outline of a conceptual scaffolding since we don’t currently know what the essential features of consciousness actually are, or what it even is. And this will lead back to speculation about the nature of angels and what their nature might be.
When Medieval philosophers like Aquinas and Scotus talked about angels they did not get into historical scholarship about the way angels were understood at the times that the biblical texts were written. Or the way angels were understood during the Second Temple period with the writing of pseudepigraphal texts like the Book of Enoch. This is a fascinating subject and on this subject I’d recommend the work of Michael S. Heiser in his books Angels and The Unseen Realm. In Biblical texts angels are messengers. That’s what the Greek angelos (ἄγγελος) means. Also the Hebrew malak (מֲלְאָךְ). There’s not much information given about their metaphysical nature. But it is their metaphysical nature that is most interesting to the Medieval philosophers.
The most important attribute of angels for philosophical purposes is that they are non-corporeal. Angels do not have physical bodies. So they are very unlike us humans. Yet they are also like us humans in a very significant aspect: they are conscious beings. They’re not only conscious but also self-conscious, intelligent, and rational, again like humans. In our regular experience we only know of one kind being that is self-conscious, intelligent, and rational: human beings. And we have good reason to believe that these attributes are essentially connected to our physical bodies and especially our brains. The idea that a being could be self-conscious, intelligent, and rational without a physical body or even just a physical brain conflicts with our regular experience. But that’s why it’s interesting.
An excellent resource on the use of angels in Medieval philosophy is Martin Lenz and Isabel Iribarren’s Angels in Medieval Philosophical Inquiry: Their Function and Significance, which is a collection of essays on the subject. In particular I recommend the chapter by Dominik Perler titled Thought Experiments: The Methodological Function of Angels in Late Medieval Epistemology. In his essay Perler works with a definition of the thought experiment from The Routledge Encyclopedia of Philosophy, given by Timothy Gooding, whom he quotes: “A thought experiment is an idealization which transcends the particularity and the accidents of worldly human activities in order to achieve the generality and rigour of a demonstrative procedure.” I think this is an excellent definition for a thought experiment. If you want to get at the essence of a concept a thought experiment is a way of looking at it in the most generalized way possible. There are certain concepts like language, rationality, and possibly self-consciousness (of the most reflective sort) that we only find in human beings. How can we think about these concepts in their general form when we only have one kind of example from actual experience? We have to use our imaginations. And so we make thought experiments.
Perler notes that thought experiments take different forms in different ages. I would say that they make use of the images that are readily available in the culture. “Today, of course, philosophers hardly speak about angels. They prefer talking about brains in the vat, brains separated from the body and sent to another planet, zombies, or people living in a black-and-whiteworld.” We take our ideas from the culture: from religion, myth, literature, and film. But are these necessarily fictional? Perler makes an interesting distinction: “Of course, one needs to make a crucial distinction when talking about thought experiments. They can be understood either as scenarios involving purely fictitious entities (e.g., brains in the vat), or as scenarios appealing to entities that have real existence or could in principle have real existence, but are considered under ideal conditions (e.g., the scientist Mary who has all knowledge about colours). Since medieval authors took angels to be real entities, endowed with real causal power and interacting with other real entities, they were certainly not interested in thought experiments in the first sense [fictitious entities]. They were rather focusing on thought experiments in the second sense, analyzing angels as real creatures that transcend the material world and therefore enable us to examine cognitive activities in its purest and most ideal form, which is not subject to material constraints.”
I mentioned before that no Medieval person really asked “How many angels can dance on the head of a pin?”. But we can find examples of something kind of close. In the Summa Theologiae Thomas Aquinas asked the question: “Whether several angels can be at the same time in the same place?” (Summa Theologiae, First Part, Question 52, Article 3) This he answered in the negative: “I answer that, There are not two angels in the same place.” I’d actually answer the question differently I think. But what’s important is that the question makes sense to ask. We assume here that angels are immaterial. So there are questions that arise regarding the relation of immaterial things to space. Does something immaterial take up space? Could it take up space under certain circumstances? If the specific question about angels seems too remote, think about other immaterial things. First, consider mathematical sentences like 1+1=2. Does that take up space? It would seem not to. It’s just not a spatial kind of thing. Second, consider a field as understood in physics? A field is “a physical quantity, represented by a scalar, vector, or tensor, that has a value for each point in space and time.” Some fields probably have actual physical existence. In quantum field theory certain fields are understood to be the most basic building block of physical reality that give rise to everything else. But other fields are more abstract, especially since we can invent all kinds of fields to suit our purposes. For example, we can imagine a temperature field where every point in a given volume has a certain scalar temperature value. This kind of field would obviously be spatial in nature since it is defined over a given region of space. But it’s not exactly a physical thing either. It’s just a set of numbers. These two kinds of immaterial things have very different relations to space. For any kind of immaterial thing, including angels, it’s reasonable to ask which kind of relation to space it has. How many mathematical sentences, such as 1+1=2, can fit on the head of a pin? In the asking of that question we can see that mathematical sentences just aren’t the kinds of things that take up space or subsist in space at all. That’s an interesting feature of mathematical sentences.
Let’s look at another Medieval example. In his article Dominik Perler looks at the work of Duns Scotus and William of Ockham on the subject of perception. They framed the issue as one of how angels could have cognition of things in the world. Physical beings perceive the world through their physical senses. But nonphysical beings wouldn’t have sense organs of this sort. They would need other sorts of cognitive devices “to make things cognitively present to them.” Both Scotus and Ockham held that “every cognition requires a cognitive act and a cognitive object.” But they had different views about what that cognitive object would be. For Scotus, “the appropriate object for an intellectual act is the essence of a thing.” For Ockham, “the appropriate object for an intellectual act is the individual thing with its individual qualities.” Both Scotus and Ockham then think about how cognitive objects become cognitively accessible. And they use angels in their thought experiments to make this as general as possible. They don’t even refer to sense perception. Rather, there’s simply something that makes the cognitive object cognitively accessible. That something could be sense perception but it doesn’t have to be. So it’s thoroughly general. For me, as a physical being with physical senses, before I cognize something like a chair I perceive it with my senses. But after I perceive it with my senses there’s an intellectual act by which I cognize it. For Scotus the object of this intellectual act is the essence of a chair. For Ockham the object of this intellectual act is the individual object, which happens to be a chair. These are two very different ways of understanding cognition. And by using angels, nonphysical beings, in their thought experiments they bracket everything that comes before the intellectual act because it’s that intellectual act specifically that interests them. It doesn’t matter if what makes the cognitive object cognitively accessible is sight, smell, echolocation, electroreceptors, or what have you. This can apply to humans, bats, sharks, computers, or angels. That’s why it’s fully generalized. They are just interested in what happens in the intellect.
So how does the cognitive object become cognitively accessible to the intellect? For Scotus, the cognitive object is the essence of a thing and “to make the essence of a thing cognitively accessible, the intellect needs a cognitive device: the intelligible species.” For Ockham, the cognitive object is the individual thing and “to make an individual thing cognitively accessible, the intellect simply needs a causal relationship with that thing.” For Scotus, “the intelligible species determines the content of an intellectual act”. For Ockham, “the individual thing itself determines the content of an intellectual act.” What does this look like in practice? I expect that Ockham’s view will seem most plausible up front. Going back to the chair example, the essence of a chair sounds kind of fictional. Isn’t it just the thing itself we’re dealing with that we then understand to be a chair? Nevertheless, I’d say that in the history of philosophy these two views are pretty evenly represented. Just to comment on it briefly, it’s arguably that our cognition always has some intentionality to it. It’s always directed towards something. We don’t just cognize the thing but also what we can do with it. A chair, for example, is not just an elevated platform with four legs and a backing. A chair is something to sit on. And it’s arguable that that usefulness is the first thing we cognize.
Perler comments that for both Scotus and Ockham, “their detailed analysis was motivated by an interest in the general structure of cognition… They both wanted to know how cognition works in principle, i.e. what kinds of entities and relations are required in any cognitive process.” The philosophy of mind understandably tends to be very human-focused. But that leaves out many other ways of cognizing, both real and imagined, from bats to sharks to computers. By using angels in their thought experiments Scotus and Ockham were able to think about these issues in a way that transcended the particularity of all these cases and think about cognition as such. I think that Medieval people had an easier time thinking about human attributes in this more general way because more of them believed in a universe populated by beings of an unseen realm that had many human-like attributes. Part of the “discarded image” as C.S. Lewis called it. The anthropologist Marshall Sahlins called these kinds of beings “metapersons”, something he proposed recovering and studying in a “new science of the enchanted universe” (see The New Science of the Enchanted Universe: An Anthropology of Most of Humanity). This worldview of a heavily populated unseen realm led Medievals to come up with useful concepts that they otherwise might not have. This is something Joseph Koterski has argued, with the case of Boethius in particular (see Natural Law and Human Nature). In his writings about these various kinds of human-like beings Boethius had to come up with a technical term and stipulate an appropriate definition to refer to all of them, both human and non-human. He used the term “person”, which he defined as an individual substance of a rational nature. A wonderfully general definition that preserves the essential core.
Could we make similar use of angels in modern thought experiments? I think they could be used in a similar way as used by the Medievals, i.e. to transcend the particularity and accidents of human beings and explore concepts in their most general form. One topic that interests me and where I can see application of this is to consciousness, or more especially self-consciousness. This is a distinction that Roger Scruton has made (see The Soul of the World, p. 40). Consciousness is the state of being aware of and able to perceive one’s environment, thoughts, and feelings. This is something that many animals would seem to have. Self-consciousness is a higher level of awareness where an individual is not only conscious but also aware of themselves as a distinct entity with their own thoughts, feelings, and identity. It involves reflection on one’s own mental states and actions. Humans are certainly self-conscious. As humans we know this because we have direct, first-person access to this higher level of awareness and reflection. And we assume, rightly and non-solipsistically, that this is common to other humans as well. We can also talk to each other and infer from our conversations that we share this self-conscious nature. Other animals might be self-conscious in this way as well. Or they might not be. We don’t really know because we are not of the same species and we can’t talk with them. No other animals have language. It’s possible we Homo sapiens are unique in our self-consciousness.
Let’s consider a progression of abstraction from human consciousness to hypothetical consciousness in other physical beings, to general consciousness as such, abstracted from all particular instances.
We start with human beings. We know a lot about human physiology, psychology, and neurology. All these contribute to the human experience, including our experience of self-consciousness. We know our mental operations are highly if not entirely dependent on our brains. At a very basic level our brains are composed of neurons and the synaptic relations between neurons. Our brains are also further organized into structures whose activity we can observe under various scenarios and activities. We’ve amassed a good deal of knowledge about our brains but there is still a great deal we don’t know. And ultimately we don’t have an answer to what David Chalmers has called the “easy problem of consciousness”: how all our mental experiences like perception, memory, and attention correlate to specific brain mechanisms and processes. We don’t have a complete “map” of the brain. We can’t read people’s minds by looking at their brains. So we still have to speak in rather general terms.
I think the next step removed from human beings would be other species that are closely related to us in the genus Homo. Unfortunately all other species of our genus are extinct so we can’t observe them or talk with them. It’s reasonable that it may have been possible to talk to some of them. Neanderthals seem to have been very similar to humans. They may have had very similar brains, similar enough to have similar capabilities but different enough to be interesting and to make some generalizations about our common features. That’s no longer possible, but that was a very close step removed from human beings that would have been useful for generalization.
To move another step from humans we may have to look beyond our planet and our evolutionary relatives. This would be an organic alien lifeform. We may never encounter such a being but I put it before an artificial lifeform, which we may encounter much sooner, simply because we can imagine such beings being, for lack of a better word, organic: organisms composed of organic molecules with water-based biochemistry, probably composed of cells, with genetic information encoded in molecules, and evolutionary history. Basically, not computers or machines. We can only speculate what such beings might be like. And I suspect we’ll have more insight into the nature of their consciousness after we develop artificial consciousness, for reasons I’ll explain. What might their brains be like? Would they have the basic cellular unit (like neurons) with a complex structure built up on the relations between them?
The next level removed would be beyond any organic physical entity, human or alien, to artificial entities: artificial intelligence or artificial consciousness. The consciousness of artificial consciousness would be considered artificial because it would not be naturally occurring but instead be a product of human engineering and design. What I’m talking about here is not just artificial intelligence of the sort that started showing up everywhere in 2023, when it seemed like almost everything was getting AI capability of some kind. These are large language models (LLMs) like ChatGPT. A large language model’s artificial intelligence processes and generates human-like text based on patterns learned from large sets of text data. But LLMs lack actual awareness and subjective experience. Artificial consciousness, on the other hand, would entail a system having self-awareness, subjective experiences, and a sense of understanding its existence and environment.
We may well encounter artificial consciousness before we encounter alien life. So even though alien life might be more similar to us, being organic, if we don’t encounter it we won’t be able to learn much from it or make comparisons to the particular physical features that give rise to their consciousness. Nevertheless we may be able to infer certain features that a self-conscious alien species would have to have from features held in common between human consciousness and artificial consciousness.
What might be analogous to the brain in artificial consciousness? We can imagine that an artificial consciousness would have physical similarities to modern computers. They would probably have processing units and memory systems. Although existing artificial intelligence in the form of large language models may not be conscious, artificial consciousness may end up having similar features like a neural network structure consisting of layers of interconnected nodes (like neurons) that process data through weighted connections.
What kinds of features would be held in common between all sorts of conscious entities: humans, Neanderthals, aliens, and artificial consciousness? Right now we can’t know. But we can speculate. I suspect that there will be some kind of structure common to all. This might not be the case, which would be very confusing indeed. But let’s suppose there would be some kind of common structure. I would further speculate that it would have the form composed of basic objects plus the relations between objects. For example, in human brains the basic object is the neuron. And the brain is organized as a system of relations between neurons, the synapses. What constitutes the object and the relations might be rather different from one entity to the next. But I suspect that basic structure will apply to all conscious beings. The definition of the structure will be very complex. It’s not just that there are objects and relations between objects. Many structures would meet that description without being conscious. For example, a three-dimensional matrix of neurons in which every neuron was simply connected synaptically to its nearest neighbor wouldn’t be much of a structure. Consciousness-producing structures are much more complex. In all these cases so far each entity is physical and has some consciousness-imparting structure. In Aristotelian terms these entities are composites of matter and form, a notion called hylemorphism. In each case there is a material substratum for the consciousness-producing form or structure.
This brings me to the final level of abstraction where we pull away the material substratum leaving only the consciousness-producing structure itself; the form without the matter. This moves beyond all physical conscious entities to the completely abstract and nonphysical. The features that I’ve speculated are held in common between conscious entities have the features of a mathematical structure: a set of objects having some additional features such as relations between objects. Fully abstracted, the actual objects themselves don’t matter. These instead become open slots. This is how Verity Harte describes structures generally. Structures are the sorts of things that make available open slots that can be filled by particular objects. When the slot is filled by a physical entity, like a neuron, the structure has a particular physical instantiation. But when the slot is empty the structure is abstracted from physical instantiation. Here the structure is at its most generalized state.
The highest levels of abstraction bring up some interesting philosophical issues. Let’s start with artificial consciousness. Here the question of the number of angels dancing on the head of a pin, or the matter of space, comes up again. The volume of an adult human brain is around 1300 cubic centimeters. That’s not even counting the rest of the body that’s needed for the brain to survive and operate. Our consciousness requires space to operate. Artificial consciousness would also take up space. Maybe a single artificial conscious entity would require even more space than a human body or human brain. But let’s hope that it could be less. Could there be a kind of corollary to Moore’s Law for consciousness. Moore’s Law is the trend in the semiconductor industry for the number of transistors in integrated circuits to double every two years. Since individual transistors are being made to be progressively smaller, more can fit in a given area. Could an artificial consciousness fit in the volume of a modern smartphone? Or maybe even smaller? Could multiple artificial consciousnesses fit on the head of the pin? That might give renewed relevance to the never-actually-asked question of angels dancing on the head of a pin. How many artificial consciousnesses could operate in a space the size of the head of a pin?
Artificial consciousness also brings up questions about embodiment. In humans this is a question of the way our minds relate not just to our brains but to our whole bodies and even to our environments. Hubert Dreyfus was an important contributor to philosophical work on this question, notably in his book What Computers Can’t Do. Dreyfus was drawing on the thought of Martin Heidegger. Maurice Merlau-Ponty would also be relevant to the subject. Dreyfus referred to Heideggerian concepts such as being-in-the-world, ready-to-hand, present-to-hand, and mood to explain the necessarily embodied nature of consciousness. Dreyfus argued that human understanding is fundamentally embodied and situated in a social and physical context, that much of human expertise is tacit and non-reflective. We tend to be very brain-centered in our thinking about human beings. But we are much more than just our brains. If a human brain could be separated from the rest of the body and survive it’s hard to speak for that quality of life, if it could even qualify as a life. Notably, even Dreyfus wasn’t arguing that artificial intelligence or artificial consciousness weren’t possible. Just that they would have to have those sets of features he identified. Would an artificial consciousness then require not only processing and memory but also motility and some form of embodied existence in the world?
Then there’s the highest, nonphysical level of abstraction. An abstract, nonphysical entity that has all the essential structures of consciousness. What is the nature of such an abstraction? Could such an abstract entity actually be conscious? Or would it have mere hypothetical consciousness, in the event that the open slots happen to be filled by physical objects? Does it even make sense to think of such nonphysical, abstract entities as existing at all? This last question is the basic question of platonism? Do abstract objects in general have any existence when we’re not thinking about them or using them in some way?
We can imagine the case where this nonphysical abstraction only becomes conscious when it is physically instantiated. It’s embodied in some way, whether that body by organic or computer. This would be like the relationship of the concept of a machine to the machine itself. We might have the concept of a machine like an engine but this concept doesn’t actually perform work. For that we actually need to build the physical machine. But even with the abstract concept of a machine we could say true and false things about it. Any concept for a steam engine, for example, has to have features for heat addition, expansion, heat rejection, and compression. Any concept lacking these features could be said to be nonfunctional, even in the abstract. In the abstract neither the concept for the functional design nor the nonfunctional design produce any work. But if we were to build them, one would work and the other would not. A philosophical angel might be the same way. It’s not actually conscious in the abstract but the abstract structure would be conscious if it were physically instantiated. So we can still refer to it, like Scotus and Ockham, and talk about cognition and consciousness, and how they would work in any kind of physical instantiation, be it human, Neanderthal, alien, or computer.
Or we can imagine the more extravagant case where this nonphysical abstraction actually is conscious, even when unembodied. That’s difficult to imagine. And there are a number of objections we can make. Maybe not the most obvious of these objections but one I think is important is the matter of temporality. Consciousness seems to be essentially temporal in nature. It’s a process. Our brains aren’t static but change from moment to moment. And our brain states are constantly changing. So how would a nonphysical abstraction do the things that conscious entities do across time? We think of abstractions as being atemporal. They don’t ever change. That’s true in a sense. They don’t change with respect to actual time. But some abstract objects could have multiple elements that are organized in a way like a process. For example, an algorithm with multiple steps is a kind of process. The steps in an algorithm aren’t moments in time but they have an ordering and sequence similar to temporal processes. To take another example, a piece of music, when played, is played in time. But we can also look at a whole page of music at once. In the abstract the piece of music is no longer temporal, but it still has order and sequence.
Another objection is that it seems like a nonphysical abstraction just isn’t enough. It needs something more. Stephen Hawking put this thought quite poetically in A Brief History of Time: “Even if there is only one possible unified theory, it is just a set of rules and equations. What is it that breathes fire into the equations and makes a universe for them to describe? The usual approach of science of constructing a mathematical model cannot answer the questions of why there should be a universe for the model to describe. Why does the universe go to all the bother of existing?” Of philosophical angels we might ask, what breathes fire into them? Do they need physical instantiation to be conscious?
In the foregoing I’ve also operated under an assumption that consciousness is a structure of some kind. And that we find these kinds of structures instantiated in multiple ways that constitute individual conscious beings. This is reasonable. We always find them together. We don’t observe human consciousness without human brains. But what if that assumption is not correct? Maybe consciousness is not the structure but the structure is a condition for consciousness. And consciousness itself is something more basic. Maybe consciousness itself is a kind of monad, a fundamental, indivisible unit that possesses perception and self-awareness. A theory of such monads was developed in the thought of Gottfried Wilhelm Leibniz. There are some modern theories based on the idea that consciousness might be a basic component of the universe, rather than something reducible to anything else. Not a structure but a unit. See David Chalmers as one prominent philosopher in this area. That’s a very different picture.
In the monad view the complex structures associated with brains and computer systems would not have some structural essence identical to consciousness. Instead they might produce conditions under which it can appear. As an analogy, a generator built to create an electric current has a complex structure. But this structure is not the electric current. The electric current is something else, and something much simpler. The generator produces the conditions under which an electric current can appear. But neither the generator nor its structure are the electric current itself.
In all of this my thoughts about angels have been instrumental. Not so much a question about what actual angels might be like, but about the utility of a certain concept of angels for philosophical exercises. But what of actual angels? Could any of these ideas about angels be correct about actual angels? Granted, that question will only be interesting if you think angels might actually exist. Well, I do. So it is an interesting question for me. I like to think these kinds of metaphysical speculations are on the right track. But I definitely won’t make any strong claims to that effect. As in scripture, the angels will just have to tell us themselves what they are like, if they feel so inclined.
But to be honest what got me onto this whole subject and thinking about it was just that derisive line about angels dancing on the head of a pin. I enjoy reading Medieval philosophy and I just don’t find the characterization of their thought as endless circling around useless questions to be at all accurate. Their thinking was deep and touched on the most foundational issues of knowledge and existence. And when they did talk about angels they were talking about timeless issues on the subjects of cognition, individuation, and language. So one response to the derisive line could be that it’s not really the “own” you think it is. Medieval philosophers didn’t actually ask how many angels could dance on the head of a pin. But even if they had, I’m sure it would have been interesting.